Las variables se usan generalmente en textos escolares sin proporcionar una experiencia introductoria que pudiera servir como base para desarrollarse en sus diferentes significados (Ursini, 1993). En matemáticas se usan generalmente los símbolos literales para representar a las variables, y éstas pueden tomar diferentes significados según el contexto.
En un estudio sobre libros de texto, Tonnenssen (1980) encontró que casi en todos ellos se define de una manera explícita o implícita el concepto de variable como un símbolo fijo, así también como un referente para un conjunto de al menos dos elementos. Martz (1982) menciona: los mismos símbolos son utilizados para denotar diferentes caracterizaciones de la variable. Por ejemplo en y=3x+2 la x puede tomar cualquier valor, pero en 2x+7=9 solo puede tomar el valor de 1. También ocurre que, diferentes símbolos son empleados para representar la misma caracterización de la variable. Por ejemplo, y=x2+6 y f(x)=x2+6. Esto contribuye a opacar las diferencias entre las distintas caracterizaciones de la variable y ocultar las condiciones que determinan dónde y cómo pueden variar su valor. Más aún, es muy frecuente que para poder resolver un problema se requiera la capacidad de interpretar un mismo símbolo literal de maneras distintas.
Küchemann (1981) reportó en su estudio que la mayoría de los alumnos trataban las letras en expresiones y ecuaciones como incógnitas específicas o “número desconocido” más que como números generalizados o como variables. Este autor menciona que 55 por ciento de los niños de 13 años encuestados afirmaron que la igualdad L+M+N=L+P+N nunca es cierta. Booth (1982, 1983) encontró una fuerte resistencia de los alumnos para asimilar la noción de letra como número generalizado. Kieran (1989) evidenció que algunos alumnos no pueden asignar significado alguno a “a” en la expresión a+3 porque la expresión carece de un signo igual y de un miembro a la derecha.
Küchemann (1981) identificó seis diferentes maneras de interpretar los símbolos literales, a saber:
Letra evaluada: A la letra se le asigna un valor numérico.
Letra no utilizada: La letra es ignorada o su existencia es reconocida pero no se le atribuye ningún significado.
Letra como objeto: Se considera la letra como una abreviación del nombre de un objeto o como a un objeto en sí.
Letra como incógnita específica: La letra representa un número particular pero desconocido y los alumnos son capaces de operar directamente sobre ella.
Letra como número generalizado: Se considera que la letra representa o es capaz de asumir distintos valores.
Letra como variable: Se considera que la letra representa un rango de valores no especificado y que existe una relación sistemática entre dos conjuntos de valores de este tipo.
Usinski, Z. (1988) menciona: el concepto de la variable en sí es multifacética. Considere estas ecuaciones, todas las cuales tienen la misma forma, el producto de dos números iguales a un tercero:
A=LW
40=5x
sen x=cosx · tanx
1=n(1⁄n)
y=kx
Sin embargo, cada uno de ellos tiene una interpretación diferente: (1) una fórmula, (2) una ecuación (o enunciado abierto) para resolver, (3) una identidad, (4) una propiedad, y (5) una ecuación de una función de variación continua (para no ser resuelto). Estos nombres diferentes reflejan diferentes usos a los que se opone la idea de variable. Solo con (5) existe la sensación de “variabilidad”, de la que surgió el término variable. Aun así, no hay tal sensación si pensamos que esa ecuación representa la línea con pendiente k y contiene el origen.
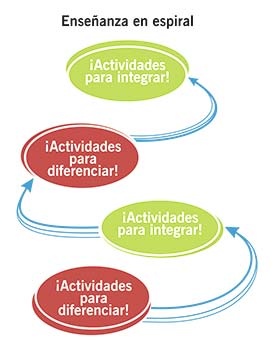
El alumno tiene dificultades con el manejo de un solo uso de la variable (como incógnita, por ejemplo), luego, al pasar a temas donde la misma letra tiene otro uso, puede tener confusión. Un problema mayor se genera cuando en un mismo problema aparece una letra con tres significados. Es por esto que Ursini (2005) recomienda que para mejorar el aprendizaje del álgebra, se realicen actividades diferenciadoras e integradoras de tres usos de la variable (como incógnita, número general y en relación funcional) para que, en un desarrollo en espiral y de lo sencillo a lo complejo, el estudiante los distinga y los integre. A esta propuesta se le conoce como el Modelo 3UV. Para conocerlo puede consultar el libro Enseñanza del álgebra elemental. Una propuesta alternativa, de la misma autora y la editorial Trillas.
Referencias
Booth, L. (1982). Developing a teaching module in beginning algebra. Proceedings of the Sixth International Conference for the Phychology of mathematics Education. Antwerp.
Booth, L. (1983). A diagnostic teaching programme in elementary algebra: Results and implications. En Hershkowitz, (eds.), 307-312.
Kieran, C. (1989). The early learning of algebra: A structural perspective. En S. Wagner y C. Kieran. Research agenda for mathematics education: Vol. 4. Research issues in the learning and teaching of algebra, 33-56. Hillsdale: Erlbaum.
Küchemann, D.E. Algebra. (1981) Children’s understanding of mathematics. Hart. K. (Ed.). London.
Martz, M. (1982). Towards a process model for high school algebra errors. En D. Sleeman & J. S. Brown (Eds.), Intelligent tutoring systems, 25-50. New York: Academic Press.
Tonnensen, L.H. (1980) Measurement of the levels of attainment by college mathematics students of the concept variable. Tesis doctoral no publicada. University of Wisconsin. Madicos.
Usinski, Z. (1988). Conceptions of School Algebra and Uses of Variables. Yearbook of the National Council of Teachers of Mathematics. Virginia: The Council.
Ursini, S (1993) Pupils’ approaches to different characterizations of variable in Logo. Thesis submitted in fulfilment of the requirement for the Ph. D. Degree of the University of London.
Ursini, S. Escareño, F Montes, D y Trigueros, M (2005). Enseñanza del álgebra elemental. Una propuesta alternativa. México, Trillas. Segunda edición.
