Es sabido que muchos jóvenes en el aula tienen problemas con el aprendizaje de las matemáticas; estos conflictos pueden deberse a diversos factores. Para su aprendizaje es necesario procesar y comunicar información, oral o escrita (texto, dibujos, diagramas, esquemas, etcétera). Sin embargo, en esta materia es común el lenguaje escrito, ya que permite la formalidad que requiere esta ciencia; otorgar ese grado de formalidad es particularmente difícil para el estudiante. Con frecuencia, las representaciones escritas están compuestas por varios elementos que obstaculizan la comprensión del mensaje. Si los docentes somos capaces de detectar tales elementos, entonces podremos otorgar el apoyo o la guía necesaria que conduzca al estudiante a la comprensión.

El estudio de las matemáticas requiere también de procesos específicos como conceptualización, análisis y reflexión, entre otros; cuando las imágenes mentales de estas actividades se representan por medio de símbolos y signos, con el fin de comunicar la información, se tiene una representación semiótica. Como en matemáticas se comunican conceptos y relaciones que existen entre ellos, se requiere de varios sistemas de expresión y de representación distintos a los del lenguaje natural o de las imágenes. Para Duval (2006) el papel de los sistemas semióticos de representación no solo es comunicar o designar objetos matemáticos, también trabajan en los objetos matemáticos y con los objetos matemáticos. Ningún tipo de procesamiento matemático se puede realizar sin utilizar un sistema semiótico de representación, porque el procesamiento matemático siempre implica la sustitución de alguna representación semiótica en otra. Duval también establece que un sistema de signos es un registro de representación si permite la representación, el tratamiento y la conversión.
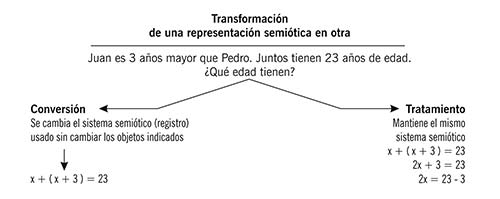
La representación ocurre cuando se señalan las características que distinguen a un objeto A, en el tratamiento se transforma una representación dentro del mismo registro, y en la conversión, se transforma la representación en registros distintos. Un ejemplo es: si se tiene el registro semiótico de un medio en el lenguaje aritmético, una representación semiótica es ½, y uno de sus tratamientos es 0.5, una de sus conversiones es 2x-1=0 porque este último se expresa en lenguaje algebraico, el cual es un registro semiótico diferente al aritmético.
Los conocimientos matemáticos que se adquieren en la escuela por lo general están sujetos a una representación semiótica, que en principio, fue una representación mental de la adquisición conceptual del objeto (noética), pero para poder crear una imagen mental, necesariamente se tuvo que observar un registro semiótico. Esta consideración muestra la estrecha interdependencia entre noética y semiótica. Duval afirma que no existe noética sin semiótica, y que la semiótica se adopta como característica necesaria para garantizar el primer paso hacia la noética. Por ejemplo, para aprender el sistema de numeración, los niños estudian los números, o mejor dicho, los grafos o símbolos que los representan. Si ellos no identifican a estos símbolos, entonces no pueden avanzar en el aprendizaje del sistema de numeración. Sin embargo, los números son los representantes y no el concepto.
Una causa de dificultad en matemáticas la señala el mismo Duval, y la denomina paradoja cognitiva de acceso al conocimiento. Con frecuencia el estudiante confunde la representación semiótica con el objeto matemático, pero dado que el objeto matemático no es tangible, éste sólo se puede conocer a través de la representación semiótica. Lo anterior se ilustra nuevamente con la conceptualización del sistema de numeración.
Un error común en la conversión de fracción a decimal es que, si tenemos 4/5 y le pedimos convertir a decimal, el estudiante realiza la división (5/4) = 1.25. Esto nos refleja la falta de una buena decodificación de la información (necesaria para la transformación). También ocurre que cuando se plantea un problema en lenguaje cotidiano y el estudiante debe elaborar un dibujo que represente la situación, le falten datos relevantes. En este último caso, se trata de una conversión de registros, del lenguaje natural al lenguaje geométrico, que al darse de manera incompleta, lleva a una solución no exitosa. Con base en los ejemplos anteriores, concluimos que, “a diferencia de las otras áreas de conocimiento científico, signos y transformación de representación semiótica están en el corazón de la actividad matemática”, “el quehacer matemático no puede desligarse de las representaciones semióticas” (Duval 2006). Entonces, ¿cómo podemos contribuir los docentes a mejorar las representaciones semióticas de nuestros estudiantes? Diferentes investigadores en educación matemática sugieren que debemos involucrar a nuestros estudiantes en actividades que les permitan construir los conceptos matemáticos a través de una variedad de transformaciones y conversiones de representaciones semióticas del objeto en estudio.
Referencia
Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational Studies in Mathematics, 61: 103–131, Springer.
http://link.springer.com/article/10.1007/s10649-006-0400-z#/page-1