Al pintar esta obra, Dalí mostró una vez más sus grandes dotes técnicas, logrando un gran colorido y un acabado hiperrealista, casi fotográfico.
Pero además realizó un profundo trabajo de composi- ción, sometiendo el lienzo a un gran rigor matemático.
Influido por la lectura de De divina proportione de fray Luca Paccioli, libro que profundiza en los principios numéricos de los pitagóricos y en
la proporción áurea presente en toda la naturaleza, el pintor decidió aplicar esas ideas a su cuadro como demuestra uno de los bocetos
conservados. Aunque a simple vista no es perceptible, el ombli- go de Gala es el centro de una circunferencia en la que se inscribe el pentagrama
místico pitagórico, que sirve para estructurar los diferentes elementos de la pintura. Igualmente aplicó la proporción áurea a la hora de dibujar
el cuerpo de Leda, el cisne, el pedestal y el paisaje. Texto e imágenes tomados de http://lamemoriadelarte.blogspot.mx/2013/02/leda-atomica.html
En una mañana del año 450 antes de Cristo los gritos de un niño rompieron la tranquilidad de Crotona. Anunciaban que el gran Hipaso de Metaponto había muerto en un naufragio ocurrido en la noche anterior. Era muy conocido en esa ciudad por su gran inventiva: hacía música con placas de metal de diferentes grosores y de distintos diámetros, y construía poliedros regulares como nunca antes se habían visto (fue él el primero en encontrar un método para inscribir un dodecaedro regular en una esfera). Pocos sabían que precisamente su genial cerebro lo había convertido en un peligroso subversivo y que ese naufragio no fue casualidad: durante varias semanas antes había estado cabizbajo y no quería asistir a las reuniones de La Hermandad. Los otros miembros de la secta sospechaban que el filósofo de Metaponto seguramente había descubierto algo muy importante, pero sólo recurriendo a los extraordinarios encantos de una irresistible y bella dama, quien embriagó y sedujo al sabio, fue que obtuvieron el gran secreto, una verdadera blasfemia contra el inolvidable Maestro Pitágoras: Hipaso demostró que existían por lo menos dos segmentos que no son conmensurables: la diagonal y el lado de un mismo pentágono regular.
Se dice que dos segmentos A͞ ͞B y C͞ ͞D son conmensurables,si existe un segmento ͞E͞F que cabe un número entero de veces en A͞ ͞B y un número entero de veces en C͞ ͞D, es decir, si las longitudes de los segmentos A͞B ͞C͞D y E͞ ͞F son a, b y c, respectivamente, entonces existen números naturales m y n tales que a = mc y b = nc. Los segmentos ͞A͞B y ͞C͞D son inconmensurables, si no son conmensurables.
En estos tiempos en que tenemos claro el concepto de número real y sus propiedades y que podemos su-mar, restar, multiplicar y dividir números reales con extrema soltura, no es difícil percatarse de que, sidos segmentos A͞ ͞B y C͞ ͞D son conmensurables, entonces la razón de sus longitudes es un número racional, es decir, es el cociente de dos números enteros y que también se cumple la proposición recíproca: si la razón entre las longitudes de dos segmentos es un número racional, entonces ellos son conmensurables. Así que demostrar que existen segmentos inconmensurables equivale a demostrar que existen números irracionales.
La introducción a este escrito es un tanto ficticia, un ardid para interesar al lector en la figura de Hipaso de Metaponto, pero no está tan alejada de las investigaciones históricas sobre este pe
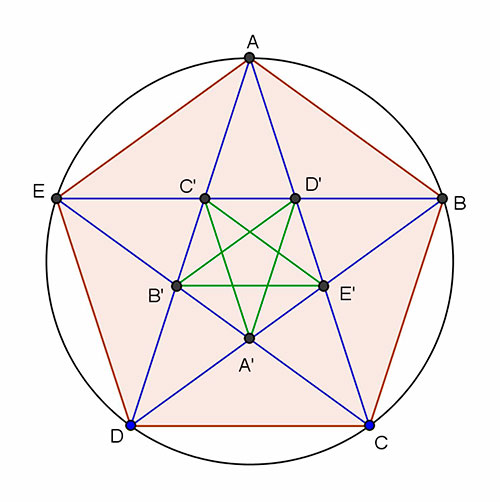
rsonaje, del cual se conoce realmente muy poco. Morris Kline menciona en su libro Matemáticas. La pérdida de la certidumbre (Editorial Siglo XXI) que, “según una vieja leyenda, los pitagóricos viajaban por mar y que uno de ellos fue arrojado por la borda por haber encontrado un elemento del universo que contradecía la doctrina pitagórica de que todos los fenómenos del universo se pueden reducir a números enteros” (y a cocientes de números enteros, es decir, a números racionales). Kurt von Fritz, en su interesante artículo The discovery of inconmensurability by Hippasus of Metaponto (Ann. Math. (2) 46 (1945), 242-264), ofrece plausibles argumentos para afirmar que el descubrimiento de la inconmensurabilidad fue hecho por Hipaso de Metaponto alrededor del año 450 a.de C., y no en el cuadrado, sino en el pentágono regular. En otras palabras, von Fritz piensa que los primeros dos segmentos inconmensurables descubiertos en la historia de la humanidad, no fueron la diagonal y el lado de un cuadrado, sino la diagonal y el lado de un pentágono regular, lo cual equivale a que el primer número irracional no fue √2, como suele creerse, sino el número áureo ᶲ = (1+√5)/2. Según. Según Von Fritz, el pentágono regular era, para los pitagóricos, una figura más misteriosa que el cuadrado. Si se intersecan las diagonales de un cuadrado obtenemos simplemente un punto, pero si se trazan todas las diagonales del pentágono no se intersecan todas en un punto, sino que forman un pentágono más pequeño que tambiénserá regular, y si se trazan ahora las diagonales de éste, se obtendrá un pentágono regular más pequeño aún, y así sucesivamente, en un proceso interminable o que involucra al infinito. Todo esto lo conocían los pitagóricos desde tiempos del Maestro Pitágoras, es decir, desde el siglo VI a. de C. y les fascinaba tanto, que la hermosa estrella pentagonal fue un símbolo distintivo de la Hermandad Pita-górica. Aún ahora se conoce a esa figura como la estrella pitagórica y sigue siendo un símbolo famoso entre los esotéricos. Sin embargo, se necesitó de una mente brillante y que estuviera familiarizada con el pentágono, para atreverse a preguntar: bueno y… ¿cuánto mide la diagonal de un pentágono regular usando como unidad su lado? o, equivalentemente, ¿cuál es la razón entre la diagonal y el lado de un pentágono regular? Así, cuando Hipaso de Metaponto encontró por primera vez en la historia de la humanidad dos segmentos inconmensurables, descubrió involuntariamente la irracionalidad de dos maneras: la existencia de los números irracionales (el número áureo) y la irracionalidad de quienes ostentan el poder, que los lleva a quitar de su camino a los seres cuyo certero pensamiento hace temblar los frágiles cimientos que los sostienen allí.
Recomendamos los siguientes textos, aparte del libro de Morris Kline y del artículo de von Fritz citados en el texto, a quien quiera conocer más acerca de este fascinante descubrimiento, considerado por casi todos los historiadores como “La primera gran crisis en la historia de las Matemáticas o, incluso, de la Filosofía”.
C. H. Edwards, Jr. The Historical Development of the Calculus, Springer Verlag, New York, Heildelberg, Berlin, 1937.
H. Eves, An Introduction to the History of Mathe-matics, Holt, Rinehart and Winston, NewYork, Fourth Edition, 1976.
H. Eves, Great Moments in Mathematics (before 1650), The Mathematical Association of America, 1980.
B. Rittaud, Qué irracional. El fabuloso destino de √2, Consejo Nacional para la Cultura y las Artes, Colección QED, Cd. de México, México, 2009.
