En cualquier trabajo técnico o profesional la imaginación puede ser mejor que la experiencia, aunque, en el reclutamiento de personal, es más solicitada la experiencia que la imaginación. La combinación de ambas es la mejor herramienta para casi cualquier actividad de los seres humanos.
La imaginación la desarrollamos desde pequeños y depende de nuestra educación, de nuestros amigos, de los juegos, de las escuelas a las que asistimos, de los libros que leemos, entre muchos otros factores que la afectan. Uno de los más grandes científicos de toda la historia, Albert Einstein, dijo: “La imaginación es más importante que el conocimiento”.
Mientras que la experiencia es la acumulación de todo tipo de conocimiento, esto es, lo aprendido con el crecimiento propio del individuo, en los juegos, en la socialización, en la escuela, etcétera, conocemos el dicho “más sabe el diablo por viejo que por diablo”, es decir, más sabe por la acumulación de conocimiento con los años, que por ser el mismo diablo.
Otro concepto importante en el desarrollo de los seres humanos es la capacidad de abstracción, del latín abstractio, vinculado al verbo abstraer (separar las propiedades de un objeto a través de una operación mental). Este concepto es fundamental en el desarrollo de habilidades mentales.
Así las cosas, todos los seres humanos, en diferente medida, tenemos imaginación, experiencia y capacidad de abstracción.
Por otro lado, una ilusión se trata de un concepto o de una imagen que surge por la imaginación o a través de un engaño de los sentidos, pero que no es real. Inclusive puede engañar a la experiencia y a la capacidad de abstracción.
Algunas de las ilusiones, o engaños a nuestros sentidos, son producto de nuestra experiencia y asociación inmediata, no consciente de la posibilidad de engaño a nuestros sentidos. De estos hay muchos ejemplos en páginas web y en libros de texto. Vemos palabras con faltas de ortografía, pero entendemos el contenido; peor, vemos textos completos mezclando letras y números, y podemos comprender el texto.
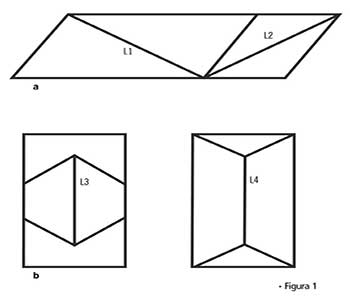
En el contexto de las matemáticas y la física la imaginación es fundamental: la experiencia se gana como cualquier otra, pero no hay cabida para la ilusión. Hagamos un experimento con la figura 1a. ¿Cómo son las líneas L1 y L2? Solo use su experiencia visual y, si quiere, su imaginación. ¿Qué puede decir de las líneas L3 y L4 de la figura 1b? Si no conoce el experimento pudo haber afirmado que L1 es mayor que L2, y que L3 es menor que L4. Con estas respuestas podía no haber alcanzado la máxima calificación de un examen, o podía haber construido algo con dimensiones equivocadas. Use una regla y mida las cuatro líneas. Al medir encontró que L1 = L2 y L3 = L4. Éste es un claro ejemplo de lo fácil que es engañar a nuestros sentidos, en particular al visual, aun cuando tengamos mucha experiencia.
Estas ilusiones se conocen con los nombres siguientes: ilusión de Sander (Fig. 1a) e ilusión de las Líneas Verticales (Fig. 1b). Existen otras ilusiones similares como train tracks o which soldier is taller, pero también existen otras más que logran que nuestro cerebro interprete dibujos que se mueven o ver más de una cara.
En el caso de figuras geométricas todos podemos diferenciar visualmente un cuadrado de un pentágono o de un hexágono. Quizá para más de 12 lados será necesario contarlos para distinguirlos del de 13, y a éste del de 14, y así. De un cuadrado sabemos que sus lados son iguales, y si le asociamos dimensiones físicas, podemos cortar uno de papel de 10 centímetros de lado, o uno de madera de 1 metro de lado; podemos imaginar una “manzana” del centro de la ciudad de Puebla que son cuadrados de 100 metros de lado, etcétera. Lo mismo pasaría si asociamos cantidades físicas al pentágono, hexágono, o cualquier figura geométrica de lados iguales. Vemos que no tenemos problemas para abstraer visualmente una forma geométrica, y asociarla a cantidades físicas; solo basados en nuestra experiencia.
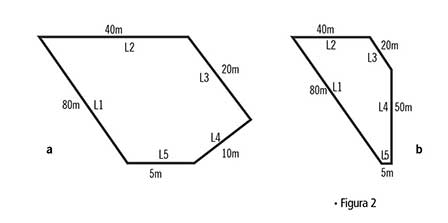
Sin embargo, en el caso de figuras irregulares, ¿qué puede suceder con la experiencia visual, la abstracción, y la realidad? En la figura 2 hay dos polígonos irregulares de cinco lados (L1 ≠ L2 ≠ L3 ≠ L4 ≠ L5). Como figuras geométricas las dos son verdaderas (ambas de cinco lados diferentes). Son verdaderas porque se puede constatar que las dos tienen cinco lados y son diferentes. Supongamos que son terrenos y que les piden marcar las mojoneras (marcas de límites entre terrenos). ¿Cuál de los dos, de acuerdo a sus dimensiones físicas, puede existir en la realidad?
Para realizar el marcado de las mojoneras es necesario trazar el polígono en el terreno, y para eso tomamos una referencia, digamos la intersección de L1 con L2 (para este experimento podemos usar como escala 1 cm = 10 m). De ahí trazamos L1 y L2, con sus respectivas dimensiones (80 y 40 m). ¿Pueden trazarse los lados L3, L4, y L5 respetando esas dimensiones? La respuesta es no para la figura 2A, al menos un lado es incorrecto en dimensiones. Tracemos L3 y L5 (20 y 5 m), que son fáciles por ser paralelos a L1 y L2, respectivamente. ¿L4 puede tener dimensión de 10 m? ¿Qué está mal? Para poder completar el polígono de la figura 2A, L4 debe tener dimensión de 50 m. Por lo que el polígono que puede existir es el representado en la figura 2B.
En este problema engañamos, mediante nuestro sistema visual, a nuestra experiencia, mostrando una figura geométrica que existe en nuestro pensamiento abstracto pero no en la realidad.
Podemos suponer varias cosas alrededor de la figura 2A, que el dibujante se equivocó al trazarlo o al escribir las dimensiones (en el sentido de las manecillas del reloj cada lado es el doble que el que le sigue), que la imprenta escaló mal o que era un truco para mostrar lo fácil que es engañar a los sentidos. Lo cierto es que la figura 2A apareció en el libro de texto de matemáticas de quinto de primaria (SEP, 2011). En [1] se demuestra que los profesores de educación básica no se dan cuenta del error, y que por tanto así lo enseñan; inclusive los topógrafos tampoco detectan el error.
La experiencia nos puede llevar a cometer errores, es necesario corroborarla con las herramientas de la física y la matemática. Principalmente, los profesores de cualquier nivel están obligados a cuestionar el contenido de los libros de texto para no propagar errores como el que se cometió en el figura 2A.
Nota
Nota: el polígono de la figura 2A, con las dimensiones mostradas, no existe en la realidad. Si tratan de ajustar sus ángulos internos o externos para formar un polígono con esas dimensiones, se darán cuenta que los lados de 40, 20, 10, y 5 metros, terminarían siendo una línea recta de 75 metros y que sería imposible formar un polígono con el lado de 80 metros.
Referencia
[1]. Juárez, J. A., Hernández, L. A., & Slisko, J. (2014). Aceptando la existencia de un terreno inexistente en un problema matemático: el uso prevalente de argumentos pragmáticos por docentes de primaria. Avances de Investigación en Educación Matemática, 6, 45 – 61.
