Los objetos que nos rodean se caracterizan por ciertas propiedades (estado), por ejemplo, el azúcar es un objeto “dulce, blanco y arenoso”. A veces, las propiedades se pueden caracterizar (medir) con cierta facilidad: su altura, dureza, color, posición o velocidad, pero en otras ocasiones esto es complicado, por ejemplo: respecto al cuerpo humanos es fácil medir la presión arterial, pero es difícil identificar la causa de una presión arterial alta. Para acceder a esta información se requieren aparatos complejos que permitan describir el estado oculto del objeto. Una posibilidad es usar alguna técnica tomográfica, estas consisten en reconstruir la propiedad requerida a partir de mediciones parciales e indirectas que captan solamente las características promedio del sistema. Para dar un ejemplo consideremos un conjunto de personas encerradas en un cuarto obscuro, ¿cómo podríamos identificar la cantidad y características de estas personas sin prender la luz? Una de las posibilidades sería hacer preguntas de diferentes tipos como ¿hay hombres aquí?, ¿quién quiere comer?, etcétera e inferir (reconstruir) lo que nos interesa a partir de las respuestas. La dificultad del procesamiento de los datos obtenidos (respuestas captadas) reside en que son colectivos, es decir, se detectan todas las voces a la vez (característica promedio), por lo que se requieren de muchas preguntas distintas para obtener la información que nos interesa. Este es el procedimiento básico de la Tomografía de Resonancia Magnética, donde lo que se detecta es la cantidad y el estado de los núcleos de los átomos de hidrógeno (de las moléculas de agua) al excitarlos con pulsos del campo magnético y registrar la radiación emitida por los núcleos excitados. Otro procedimiento tomográfico (Tomografía de Rayos X) consiste en iluminar un objeto opaco con rayos X y medir (por el tiempo de retraso) la densidad media a lo largo del camino. Resulta que las densidades medias a lo largo de distintas trayectorias que se cruzan en un punto permiten estimar su densidad, como se muestra en el dibujo. Recorriendo diferentes puntos del objeto se puede obtener la distribución de densidades dentro del objeto y con esto lo que es la llamada imagen tomográfica.
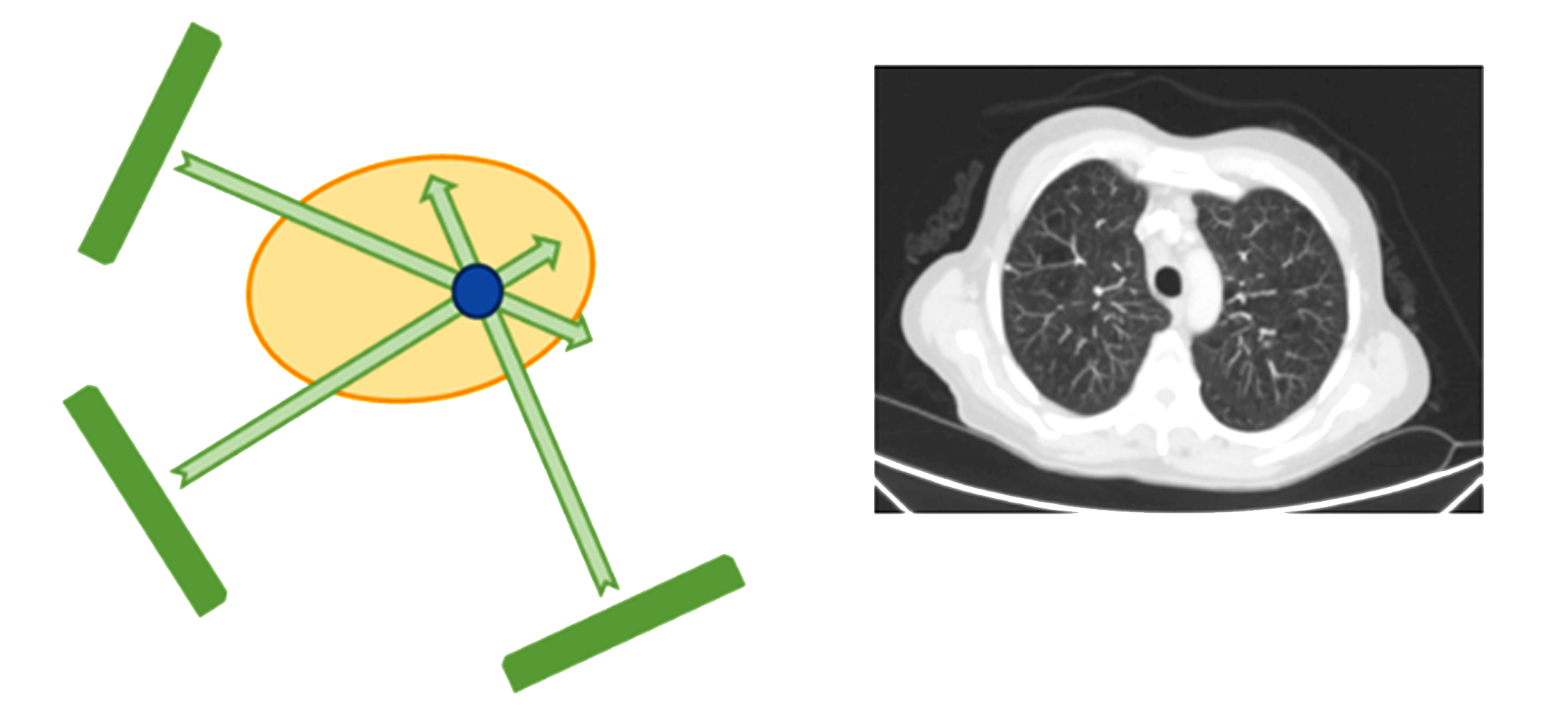
Un procedimiento similar a los anteriores se usa para determinar estados de objetos microscópicos (que se describen por leyes de la física cuántica). El mismo concepto de estado para un sistema cuántico radicalmente difiere de lo que nosotros acostumbramos observar en el mundo que nos rodea —el mundo clásico. Mientras que un sistema macroscópico se describe por el conjunto de sus propiedades (velocidad y posición de un coche), un estado cuántico (que contiene toda la información accesible) es más bien una abstracción matemática, que contiene solo información probabilística del sistema microscópico. Es decir, el conocimiento del estado de un sistema cuántico implica la posibilidad de calcular las probabilidades de que este sistema posea ciertas características. Esto sucede debido a que los objetos cuánticos tienen una propiedad muy distinta de lo que acostumbramos observar en el mundo clásico: al intentar medir alguna característica de un sistema cuántico su estado se perturba tanto que mediciones posteriores ya no proporcionan ninguna información útil sobre el estado original. Básicamente, el estado se destruye en el proceso de interacción con el aparato de medición. Además, ¡cada medición realizada sobre copias idénticas del mismo objeto puede arrojar diferente resultado!, que impone una restricción fundamental sobre la posibilidad de medir estados cuánticos directamente, por lo que la única forma de inferir el estado de un objeto microscópico es a través de un procedimiento tomográfico. Un protocolo de tomografía cuántica necesita de varios objetos cuánticos idénticos (copias del objeto) ya que cada medición se tiene que realizar sobre una copia intacta. Efectuando múltiples mediciones se obtienen ciertas características promedio de un objeto cuántico. El procedimiento tomográfico consiste en un algoritmo que permite reconstruir el estado del objeto a partir de los valores promedios obtenidos experimentalmente.
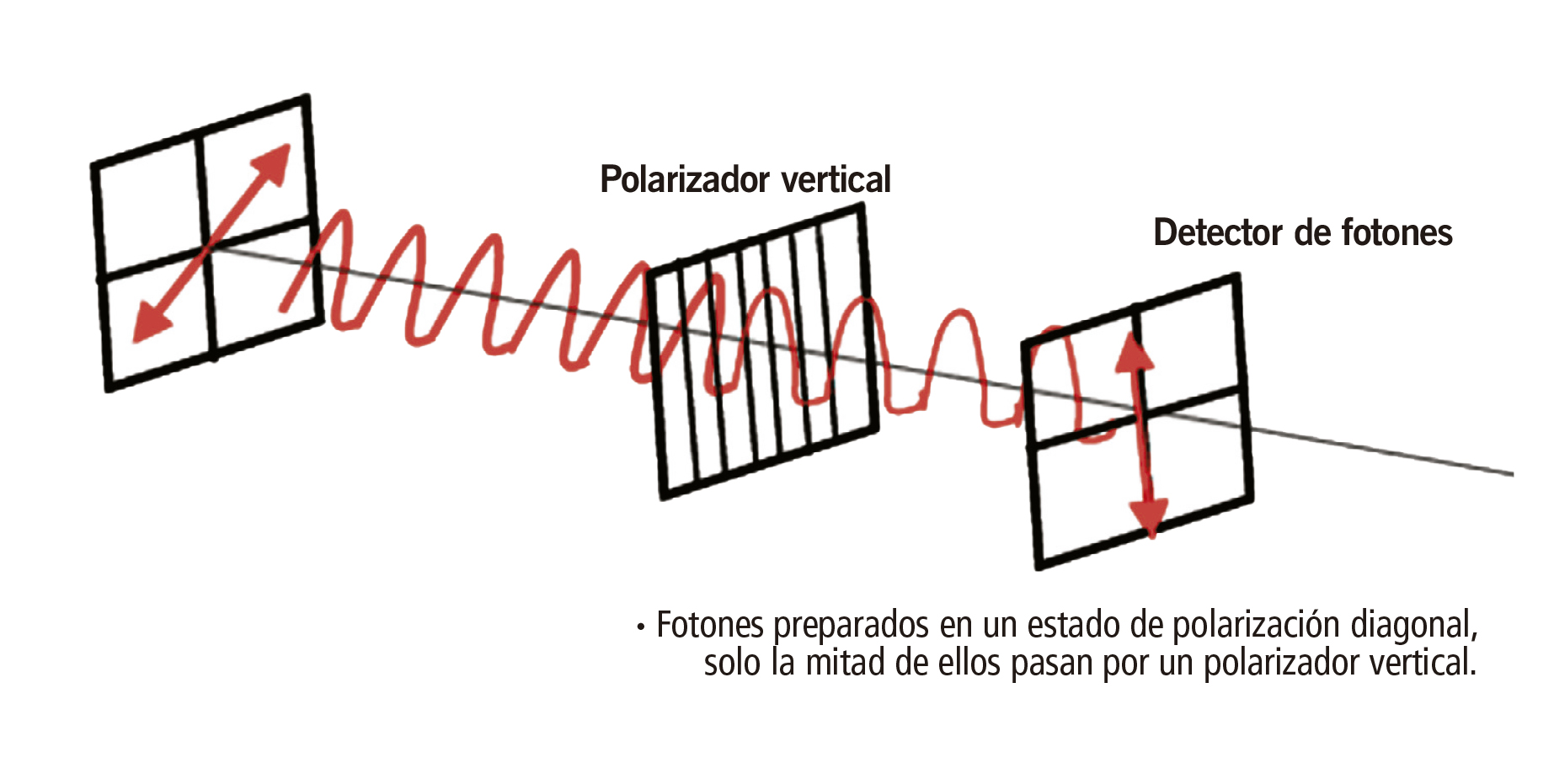
Probablemente el objeto cuántico más simple de reconstruir es el estado de polarización de un fotón (dirección de la oscilación de las ondas electromagnéticas). Todos conocemos lentes polarizados, que permiten pasar la luz solo de una cierta polarización; los ojos junto con los lentes constituyen un simple aparato de medición cuántica, ya que lo que detecta el ojo es la cantidad de fotones (intensidad de la luz) que los lentes dejan pasar.
Existe polarización horizontal, vertical y combinaciones, por ejemplo, diagonal. El fotón con una polarización vertical no puede pasar por una lente “horizontal”, pero un fotón que con una polarización diagonal tiene 50 por ciento de posibilidades de pasar a través de un polarizador (lente) vertical, esto es: la mitad de las veces veríamos los fotones pasando por los lentes. Sin embargo, no se puede predecir si un fotón específico pasará o no. Esto es un proceso estocástico que no implica algún tipo de desconocimiento, sino que es una propiedad fundamental de la naturaleza, la cual permite construir generadores de números aleatorios genuinos, encriptar información de una forma inquebrantable, etcétera.
Volviendo a la tomografía, para determinar el estado de polarización de un fotón hay que: 1) generar un haz de fotones idénticos, 2) medir la cantidad de fotones que pasan por una configuración específica de lentes: por ejemplo, detectar las probabilidades de que los fotones pasen por un polarizador vertical u horizontal (mediciones incompatibles), luego, mediante otro experimento, detectar las probabilidades que los fotones pasen por un polarizador diagonal o anti-diagonal, etcétera, observando en cada experimento solo una faceta del sistema cuántico, 3) conociendo estas probabilidades podemos reconstruir el estado de polarización del fotón. Con este estado podemos predecir todas las propiedades del fotón respecto a su polarización, en particular, nos da la posibilidad de usarlo para grabar, procesar y transmitir la información de una forma que es imposible en el mundo regido por las leyes clásicas.
¿Para qué necesitamos realizar tal proceso tomográfico? Esta es la única posibilidad de obtener toda la información accesible sobre los objetos cuánticos, que son elementos fundamentales de las tecnologías cuánticas ya existentes (teleportación cuántica, criptografía cuántica, computación cuántica, mediciones super precisas, etcétera) y futuras. Pero esto sería material para el próximo artículo.