En la enseñanza de las matemáticas nos preocupamos por conocer estrategias para que el estudiante logre el aprendizaje. En la resolución de problemas también se requieren de éstas para obtener una solución exitosa. En este artículo presentamos a la elaboración del dibujo del modelo situacional como una herramienta en la resolución de problemas contextualizados de matemáticas. Esta propuesta se basa en la teoría de van Dijk y Kintsch (1983) la cual postula que al leer un texto se trabaja con tres niveles de representación mental: el código de superficie, la base de texto y el modelo situacional. Estas etapas o niveles son parte del proceso mental de comprensión y transitan desde la identificación de las palabras, las oraciones y sus significados hasta la construcción de una imagen de la situación que se plantea en el texto. Esta imagen que se crea uno sobre lo que está leyendo, puede ser un esquema, un diagrama, un cuadro, etcétera. Para poder entender mejor qué es el modelo situacional consideremos el problema que apareció en un libro de texto de secundaria:
Cecilia participa en una competencia de salto de longitud. Si del punto límite camina 15 pasos en sentido contrario a la fosa y un paso de ella equivale a 0.70 m y su salto es de 3.80 m, ¿con qué número con signo representas el recorrido previo al salto?
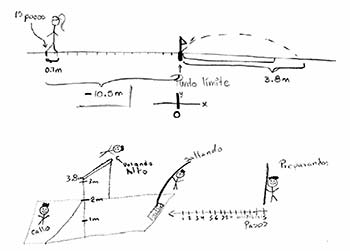
Ahora que usted ya leyó la situación y la imaginó, haga un dibujo y después resuelva el problema. ¿Su dibujo es parecido al de la Figura 1?
El modelo situacional depende mucho de las experiencias previas del lector. Al planteárselo a diferentes alumnos nos han preguntado ¿Qué es una fosa? o ¿a qué se refiere con “caminó 15 pasos en sentido contrario a la fosa”?, ¿cuál es el punto límite? Si no entendemos alguna palabra o descripción en el texto, nuestro modelo situacional podría no representar la situación planteada por el autor y, por esta razón, podríamos no obtener la respuesta correcta. Tijero (2009) afirma que la construcción de un Modelo Situacional coherente es esencial para una adecuada comprensión del texto.
En la Figura 2 podemos ver que el lector confundió el salto de longitud con un salto de altura y, como era de esperarse, no pudo resolver el problema, su modelo situacional no fue coherente con el problema.
Es por esta razón que concluimos: en problemas contextualizados de matemáticas, elaborar un dibujo permite al docente saber de qué manera el estudiante está entendiendo el problema. Además de que puede tener información sobre las dudas y los conceptos que no entiende. El modelo situacional es un paso previo al modelo matemático del problema y es un paso necesario.
Invitamos a los docentes de matemáticas a que utilicen el dibujo como una herramienta para conocer el nivel de comprensión textual de sus estudiantes, principalmente en la resolución de problemas. Les aseguramos que se llevarán muchas sorpresas.
Referencias
Tijero, T. (2009). Representaciones Mentales: discusión crítica del modelo de la situación de Kintsch. Pontificia Universidad Católica de Valparaíso. Chile
Van Dijk, T., y Kintsch, W. (1983). Strategies of Discourse Comprehension. New York: Academic Press.
1 Licenciado en Matemáticas Aplicadas y estudiante de la Maestría en Educación Matemática, FCFM, BUAP. Correo: [email protected]
2 Profesores-Investigadores de la Maestría en Educación Matemática, FCFM, BUAP. Correos: [email protected] y [email protected]
[email protected], [email protected]
Twittear